load("cosmos-processed.RData")
# again just looking at Wytham Woods here
wwoods <- subset(all_sites, SITE_NAME=="Wytham Woods")
library(mgcv)Loading required package: nlmeThis is mgcv 1.9-0. For overview type 'help("mgcv-package")'.Exercise 3: Model checking and selection
Introduction
This practical session will focus on extending the models we’ve built so far and checking them.
Preamble
We’ll first load the data, subset it and load mgcv…
(If you don’t have the data, you can download it from here.)
A simple model
Let’s fit the same model as we did in the previous exercise:
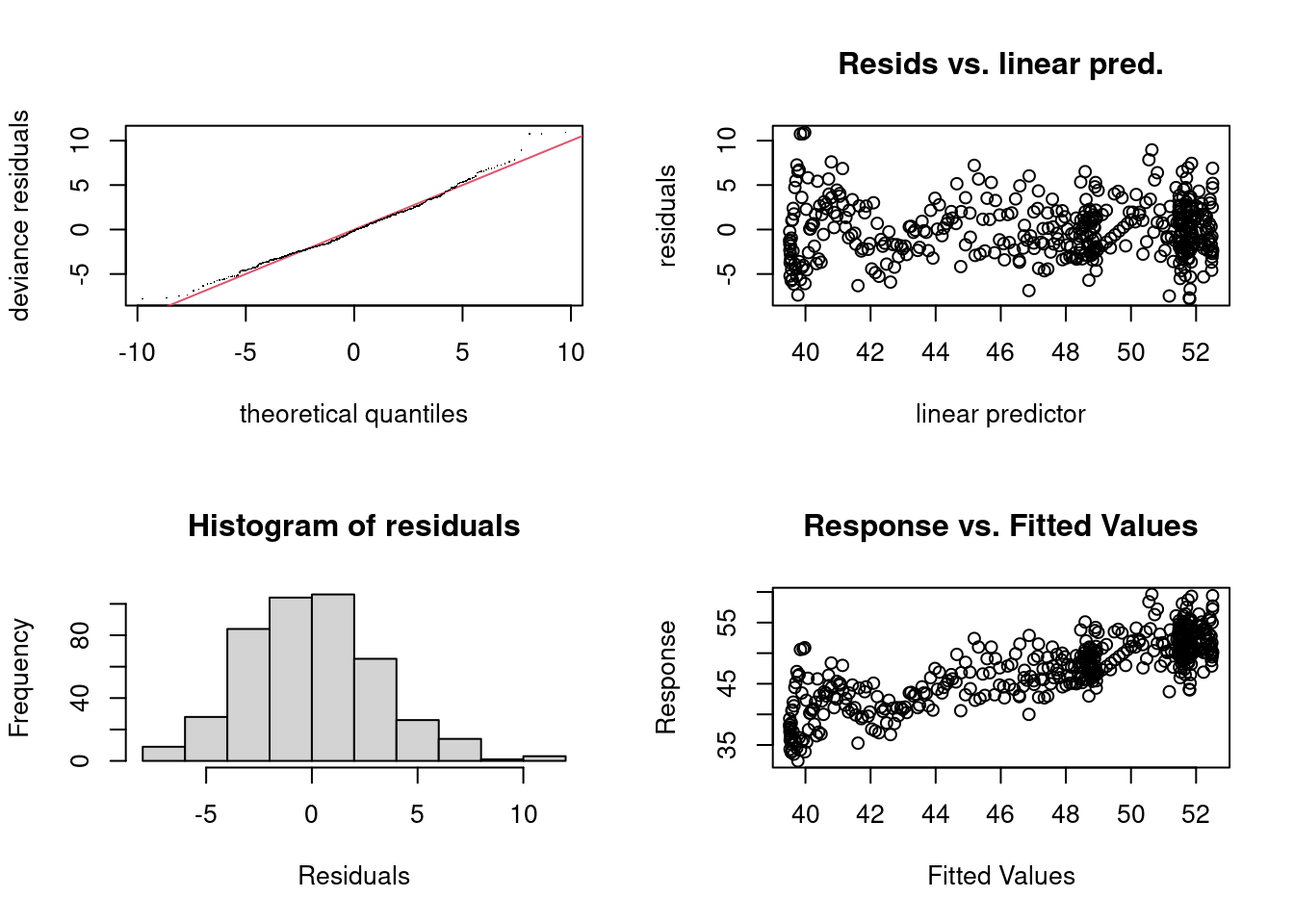
b <- gam(COSMOS_VWC ~ s(ndate), data=wwoods, method="REML")Running gam.check for the first time
We can assess the model residuals by simply looking at the output of gam.check(), so let’s do that…
gam.check(b)
Method: REML Optimizer: outer newton
full convergence after 7 iterations.
Gradient range [-3.367285e-07,8.300716e-08]
(score 1150.533 & scale 10.2183).
Hessian positive definite, eigenvalue range [3.13693,219.0595].
Model rank = 10 / 10
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(ndate) 9.00 8.17 0.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We have two bits of output here: one graphical and one text. Let’s start with the graphics:
- Top left: quantile-quantile plot of the deviance residuals, we can use this to see if the residuals are conforming to the normal distribution we would expect them to if the model is specified correctly.
- Bottom left: histogram of the deviance residuals, again allowing us to assess the normality of the residuals.
- Top right: residuals vs linear predictor, this is will highlight if there are issues with non-constant variance (heteroskedasticity). If the deviance change its spread as we increase the value of the linear predictor, then we think there might be problems with non-constant variance. In this case we have a mess of points with no clear pattern, so all is well.
- Bottom right: response vs fitted values gives a very rough idea of model fit. We would expect the points to lie on the line y=x for “perfect” prediction. This plot may also help us identify where the model isn’t fitting well.
As for the text output:
- The first block of text tells us about the optimisation process. We can ignore most of this for now.
- The rest of the text concerns whether
kis large enough for the terms in the model.k'gives the number of degrees of freedom for the term (not that this takes into account things like removing multiple intercepts for identifiability). We then haveedfgiving how many degrees of freedom the model actually used. In general we don’t want these numbers to be to close. We can test to see how close they are using the test provided here. When thek-indexis <1 and thep-valueis “low” we might need to increasekfor that smooth in the model. Note that this can be misleading for models like this, with just one covariate and where we think other things might effect model fit (like missing covariates!). (You probably noticed this in a previous practical where increasingkstill left us with a smallk-index/p-value.)
So, from this output, we can conclude that although the assumption that the response is normal seems pretty solid (though see next subsection) and we don’t have to worry about non-constant variance, we still are lacking some explanatory power in the model we fitted. We probably need some additional covariates to explain what’s really going on.
What about switching response distribution?
We can be extremely picky and investigate whether we can improve the tail behaviour in the Q-Q plot above. We can try fitting a model with a response with heavier tails, for example the t distribution.
Changing the response distribution is simple a matter of giving the family= argument and specifying we use the scaled t, scat() family:
b_t <- gam(COSMOS_VWC ~ s(ndate), data=wwoods, method="REML", family=scat())
summary(b_t)
Family: Scaled t(16.389,2.997)
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 47.2890 0.1509 313.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(ndate) 8.17 8.813 878.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.656 Deviance explained = 62.2%
-REML = 1149.4 Scale est. = 1 n = 440We can see some differences between this models’ output and the one we fitted with a normal response (which we can explicitly ask for with family=gaussian()).The Family line reflects the change and gives the estimated hyperparameters for the distribution.
We’re really interested in the effect we have on the Q-Q plot, so let’s see that side-by-side with the normal model:
par(mfrow=c(1,2))
qq.gam(b, main="normal", rep=200, asp=1)
qq.gam(b_t, main="t", rep=200, asp=1)
The difference here looks pretty marginal, so let’s stick to the normal response for now.
To see what other response distributions are available, see ?family.mgcv.
Modelling multiple sites
Let’s subset the data to get the sites in Scotland and start working with multiple variables in our model (note that the covariates that we have in the data vary between sites, so altitude or soil type will be constant within site).
scot_sites <- subset(all_sites,
SITE_NAME %in% c("Crichton", "Easter Bush",
"Hartwood Home", "Cochno",
"Balruddery", "Glensaugh"))Plotting those time series to get an idea of what we’re modelling:
library(ggplot2)
ggplot(scot_sites) +
geom_line(aes(x=DATE_TIME, y=COSMOS_VWC)) +
facet_wrap(~SITE_NAME) +
labs(x="Date", y="Soil moisture") +
theme_minimal()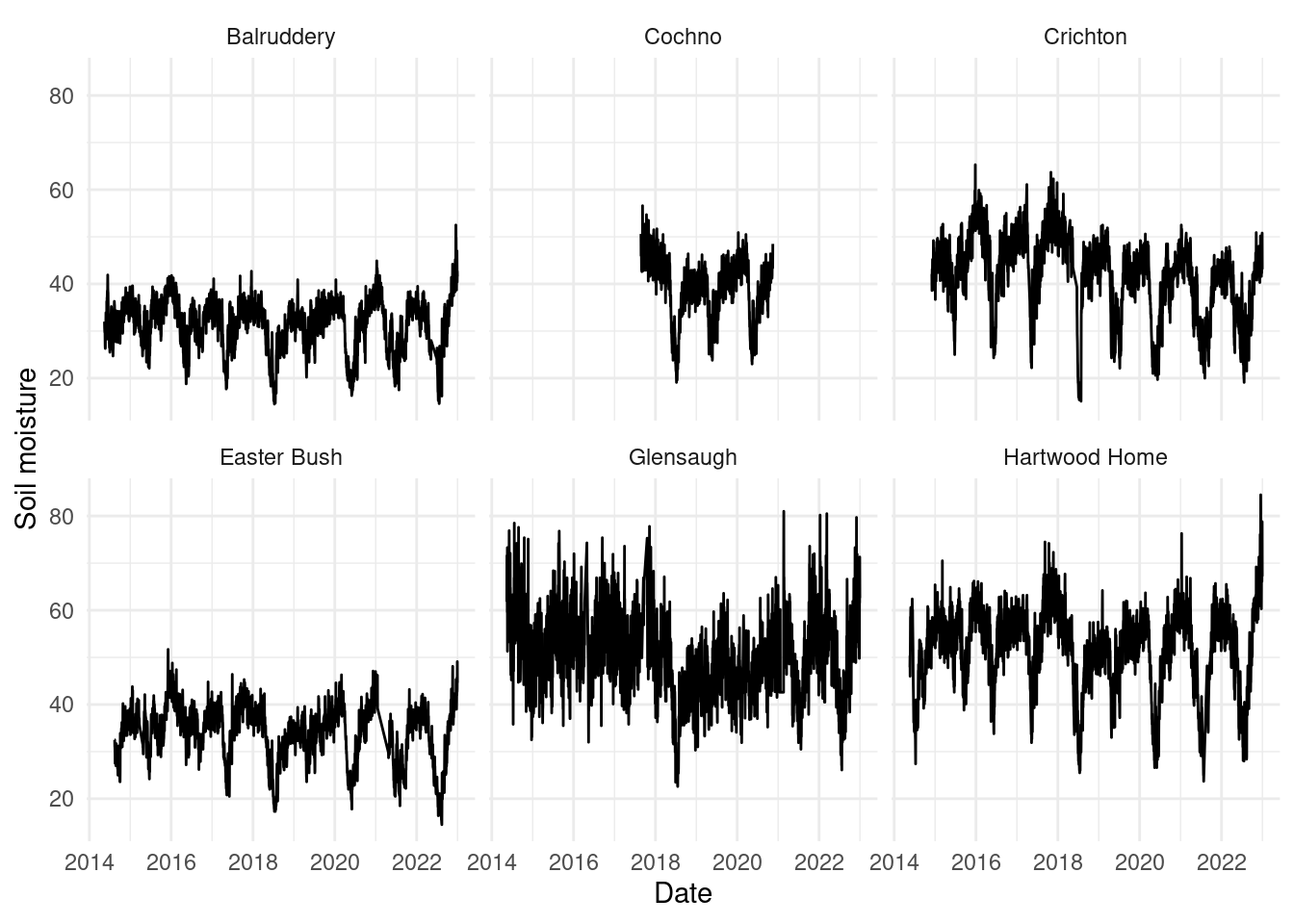
The time series for the Cochno site is very short compared to the others, so in practice we might want to check performance for this site, as estimates will be highly influenced by the other sites.
We can then fit a model with both time and the site identifier as a random effect using the bs="re" argument to specify a simple random effect. This effectively gives us a different intercept for each site.
b0 <- gam(COSMOS_VWC ~ s(ndate), data=scot_sites, method="REML")
b1 <- gam(COSMOS_VWC ~ s(ndate) + s(SITE_ID, bs="re"), data=scot_sites, method="REML")Note that since the covariates are mostly measured at the site level, the site random effect is completely confounded with soil type, altitude etc. So we can come up with a model that is superior in AIC terms:
AIC(b0, b1) df AIC
b0 10.68555 122738.4
b1 15.89472 109391.2but it might not be the most biologically/ecologically interesting one.
Adding other covariates
Let’s add some more interesting covariates instead. We have a few available, but we should check that they are available for all the data we want to model. If covariate values are unavailable (NA in R), then mgcv will (silently) drop those samples from the model. This can cause issues as 1) we don’t know what has been dropped 2) comparisons via (e.g.) AIC are not valid as the data are different between the models that are being compared.
So we’ll start by looking at four covariates: ALTITUDE, PRECIP, SOIL_TYPE and LAND_COVER. First just checking the NA status of each covariate.
# samples in the data overall
nrow(scot_sites)[1] 16208# how many have NA in ALTITUDE
sum(is.na(scot_sites$ALTITUDE))[1] 0# how many have NA in PRECIP
sum(is.na(scot_sites$PRECIP))[1] 700# how many have NA in SOIL_TYPE
sum(is.na(scot_sites$SOIL_TYPE))[1] 0# how many have NA in LAND_COVER
sum(is.na(scot_sites$LAND_COVER))[1] 0We can see here that PRECIP is a problem and we won’t be able to make AIC comparisons between models with PRECIP in vs. ones without, unless we remove those observations for all models.
At this point I’ll say don’t just do the following in general and exclude the troublesome data without thinking. In practice we’d want to check to see if there was a systematic reason why there were NA values in some places rather than others (did one site’s equipment breakdown? Is there a gap in the data due to bugs in the source CSV files?). We need to be careful in general. Here (for the sake of this being a tutorial, not a book/paper/report) we’ll throw caution to the wind and just exclude those observations though:
bad_idea <- is.na(scot_sites$PRECIP)
scot_sites <- scot_sites[!bad_idea, ]We can also look at the number of levels the SOIL_TYPE and LAND_COVER variables have:
table(scot_sites$SOIL_TYPE)
Calcareous mineral soil Mineral soil
0 12575
Organic soil Organic soil over mineral soil
2933 0 table(scot_sites$LAND_COVER)
Acid grassland
0
Arable and horticulture
2821
Arable and horticulture (previously improved grassland)
2730
Broadleaf woodland
0
Calcareous grassland
0
Coniferous forest
0
Coniferous woodland
0
Grassland
0
Heather
2933
Heather grassland
0
Improved grassland
7024
Orchard
0 These have relatively few levels, so we can probably add them as fixed effects, rather than random effects. Note that again because these two variables only vary between sites, we choose only to model LAND_COVER as it has more levels and hence potentially more explanatory power:
b2 <- gam(COSMOS_VWC ~ s(ndate, k=20) + s(ALTITUDE, k=5) + s(PRECIP, k=20) +
LAND_COVER,
data=scot_sites, method="REML")
summary(b2)
Family: gaussian
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate, k = 20) + s(ALTITUDE, k = 5) + s(PRECIP,
k = 20) + LAND_COVER
Parametric coefficients:
Estimate
(Intercept) 98.78
LAND_COVERArable and horticulture (previously improved grassland) -117.79
LAND_COVERHeather -365.86
LAND_COVERImproved grassland 72.88
Std. Error
(Intercept) 104.49
LAND_COVERArable and horticulture (previously improved grassland) 289.46
LAND_COVERHeather 498.40
LAND_COVERImproved grassland 46.07
t value
(Intercept) 0.945
LAND_COVERArable and horticulture (previously improved grassland) -0.407
LAND_COVERHeather -0.734
LAND_COVERImproved grassland 1.582
Pr(>|t|)
(Intercept) 0.344
LAND_COVERArable and horticulture (previously improved grassland) 0.684
LAND_COVERHeather 0.463
LAND_COVERImproved grassland 0.114
Approximate significance of smooth terms:
edf Ref.df F p-value
s(ndate) 18.986 19.00 656.651 <2e-16 ***
s(ALTITUDE) 2.000 2.00 0.827 0.437
s(PRECIP) 8.267 10.09 79.714 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.761 Deviance explained = 76.1%
-REML = 47934 Scale est. = 27.956 n = 15508Note that I’ve already increased k to 20, based on what we’ve previously seen.
The fixed effect of LAND_COVER doesn’t seem to be significant, so we can remove this:
b2_1 <- gam(COSMOS_VWC ~ s(ndate, k=20) + s(ALTITUDE, k=5) + s(PRECIP, k=20),
data=scot_sites, method="REML")
summary(b2_1)
Family: gaussian
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate, k = 20) + s(ALTITUDE, k = 5) + s(PRECIP,
k = 20)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 41.86020 0.05511 759.6 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(ndate) 18.977 19.00 376.22 <2e-16 ***
s(ALTITUDE) 3.998 4.00 3515.15 <2e-16 ***
s(PRECIP) 8.869 10.77 68.09 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.597 Deviance explained = 59.8%
-REML = 51982 Scale est. = 47.097 n = 15508With fixed effects we can’t use the shrinkage approach that we saw in the lecture material, so we have to resort to using p-values, as we would with a GLM.
Note that this does decrease the R^2 and deviance explained.
Looking at the gam.check() output for this model we see that the model’s residuals look pretty normal, with some deviations from that in the tails (more in the lower tail, top left Q-Q plot). There might be some slight evidence of non-constant variance (top right plot of residuals vs. linear predictor), but this is far from obvious here.
gam.check(b2_1)
Method: REML Optimizer: outer newton
full convergence after 11 iterations.
Gradient range [-0.02830836,0.0281147]
(score 51982.25 & scale 47.09726).
Hessian positive definite, eigenvalue range [1.475788,7752.041].
Model rank = 43 / 43
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(ndate) 19.00 18.98 0.81 <2e-16 ***
s(ALTITUDE) 4.00 4.00 0.62 <2e-16 ***
s(PRECIP) 19.00 8.87 0.99 0.31
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Also worth noting that if you prefer ggplot2-style graphics, you can use the gratia package to get an equivalent plot to gam.check() using gratia::appraise():
# install.packages("gratia")
library(gratia)
appraise(b2_1) + theme_minimal()
Selecting smooth terms during fitting
First let’s try using the thin plate spline with shrinkage basis (bs="ts") for all the terms in model b2_1:
b2_2 <- gam(COSMOS_VWC ~ s(ndate, k=20, bs="ts") +
s(ALTITUDE, k=5, bs="ts") +
s(PRECIP, k=20, bs="ts"),
data=scot_sites, method="REML")
summary(b2_2)
Family: gaussian
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate, k = 20, bs = "ts") + s(ALTITUDE, k = 5,
bs = "ts") + s(PRECIP, k = 20, bs = "ts")
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 41.86020 0.05511 759.5 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(ndate) 18.975 19 376.48 <2e-16 ***
s(ALTITUDE) 3.997 4 3516.54 <2e-16 ***
s(PRECIP) 8.217 19 38.49 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.597 Deviance explained = 59.8%
-REML = 52003 Scale est. = 47.103 n = 15508We can see very little difference here in terms of EDF. So, there is not much harm done by using bs="ts" as a matter of course when fitting models.
What about when it does matter? As in the slides, we can look at the case where we have SITE_ID and ALTITUDE in the same model, where we know that the covariates are confounded:
b2_c <- gam(COSMOS_VWC ~ s(ndate, k=20, bs="ts") +
s(ALTITUDE, k=5, bs="ts") +
s(PRECIP, k=20, bs="ts") +
s(SITE_ID, bs="re"),
data=scot_sites, method="REML")
summary(b2_c)
Family: gaussian
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate, k = 20, bs = "ts") + s(ALTITUDE, k = 5,
bs = "ts") + s(PRECIP, k = 20, bs = "ts") + s(SITE_ID, bs = "re")
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 41.56 3.34 12.44 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(ndate) 1.899e+01 19 2548.45 <2e-16 ***
s(ALTITUDE) 3.942e-05 4 0.00 0.232
s(PRECIP) 7.709e+00 19 61.07 <2e-16 ***
s(SITE_ID) 4.999e+00 5 6452.04 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.761 Deviance explained = 76.1%
-REML = 47963 Scale est. = 27.959 n = 15508Now there is no guarantee that SITE_ID is more “important” than ALTITUDE in the model, just that SITE_ID (which adds a parameter per site) has a better likelihood than having ALTITUDE in the model. We can see the EDF has shrunk to \approx \times10^{-5}, almost completely removing the term from the model.
Exercises
- Try working through the above using a different set of sites of your choice.
- When selecting sites, be careful to check for
NAvalues in the covariates you are planning to model and compare the time series lengths with exploratory plots. - Run models using all covariates we’ve looked at above, paying particular attention to EDF values, setting
kand assessing checking results. - Does the t distribution give better Q-Q plots for your data?