Predictions and variance

David L Miller

Biomathematics and Statistics Scotland

UK Centre for Ecology and Hydrology

What can we do?

  • Use gam() to fit a model
  • Use summary() to assess it
  • Use plot() to visualise it

Going back to our model

library(mgcv)
load("cosmos-processed.RData")

wwoods <- subset(all_sites, SITE_NAME=="Wytham Woods")

b <- gam(COSMOS_VWC ~ s(ndate, k=20), data=wwoods, method="REML")

plot(b)

Now we can fit a model,
now we are dangerous

What do we want to do with our model?

  • For linear models, we often interpret coefficients
  • We don’t have that here
  • So we usually make predictions and plots
coef(b)
(Intercept)  s(ndate).1  s(ndate).2  s(ndate).3  s(ndate).4  s(ndate).5 
 47.3525000   7.5801107  13.8527308  -4.1595358 -12.1449614  -3.0512930 
 s(ndate).6  s(ndate).7  s(ndate).8  s(ndate).9 s(ndate).10 s(ndate).11 
 -8.8018184   0.8292287  -6.1265129  -7.6962263  12.2316442   7.0850161 
s(ndate).12 s(ndate).13 s(ndate).14 s(ndate).15 s(ndate).16 s(ndate).17 
 -5.2282569   3.6549750  -0.2188604  -0.3257381   9.7677258   7.0620897 
s(ndate).18 s(ndate).19 
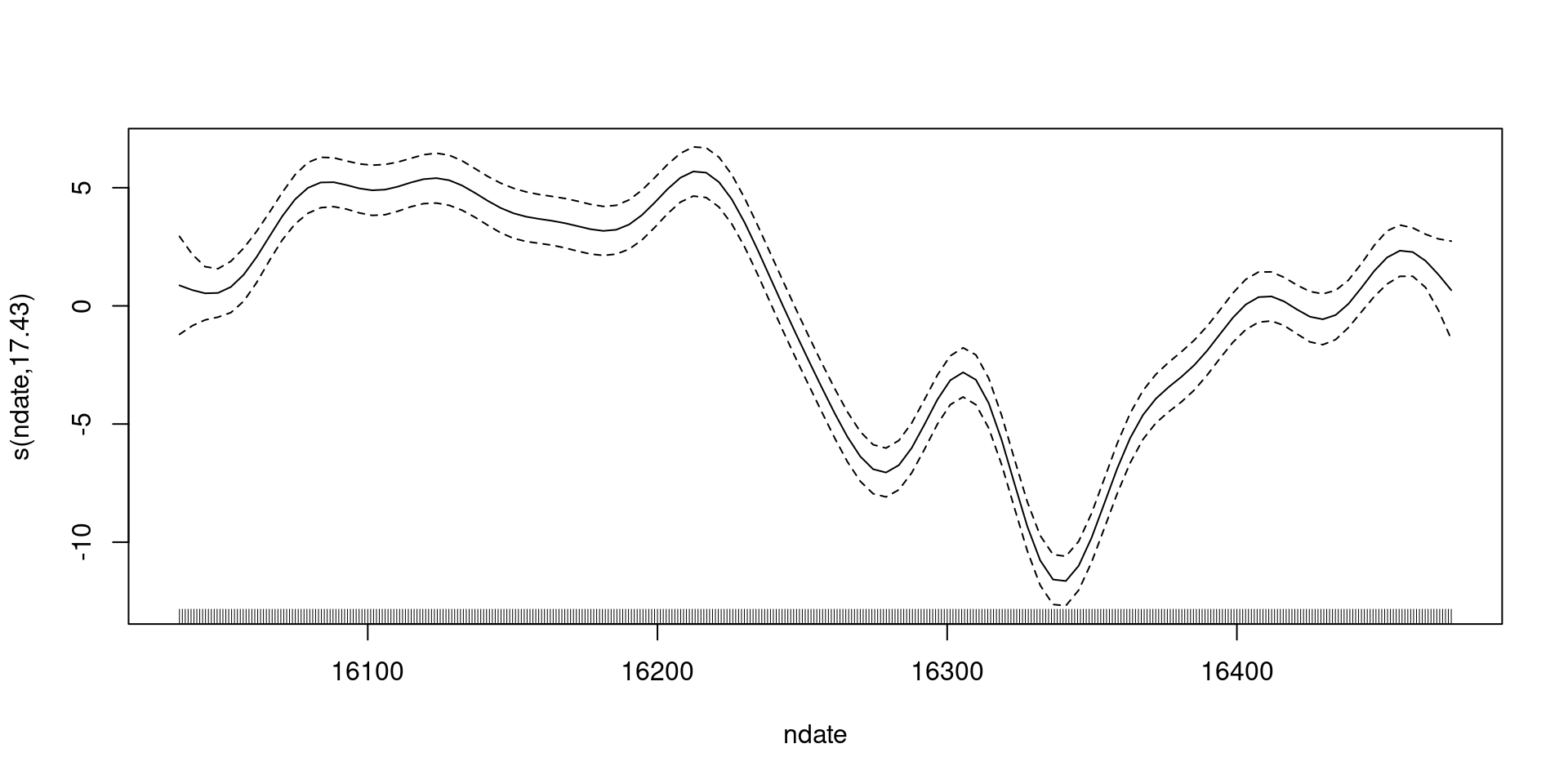
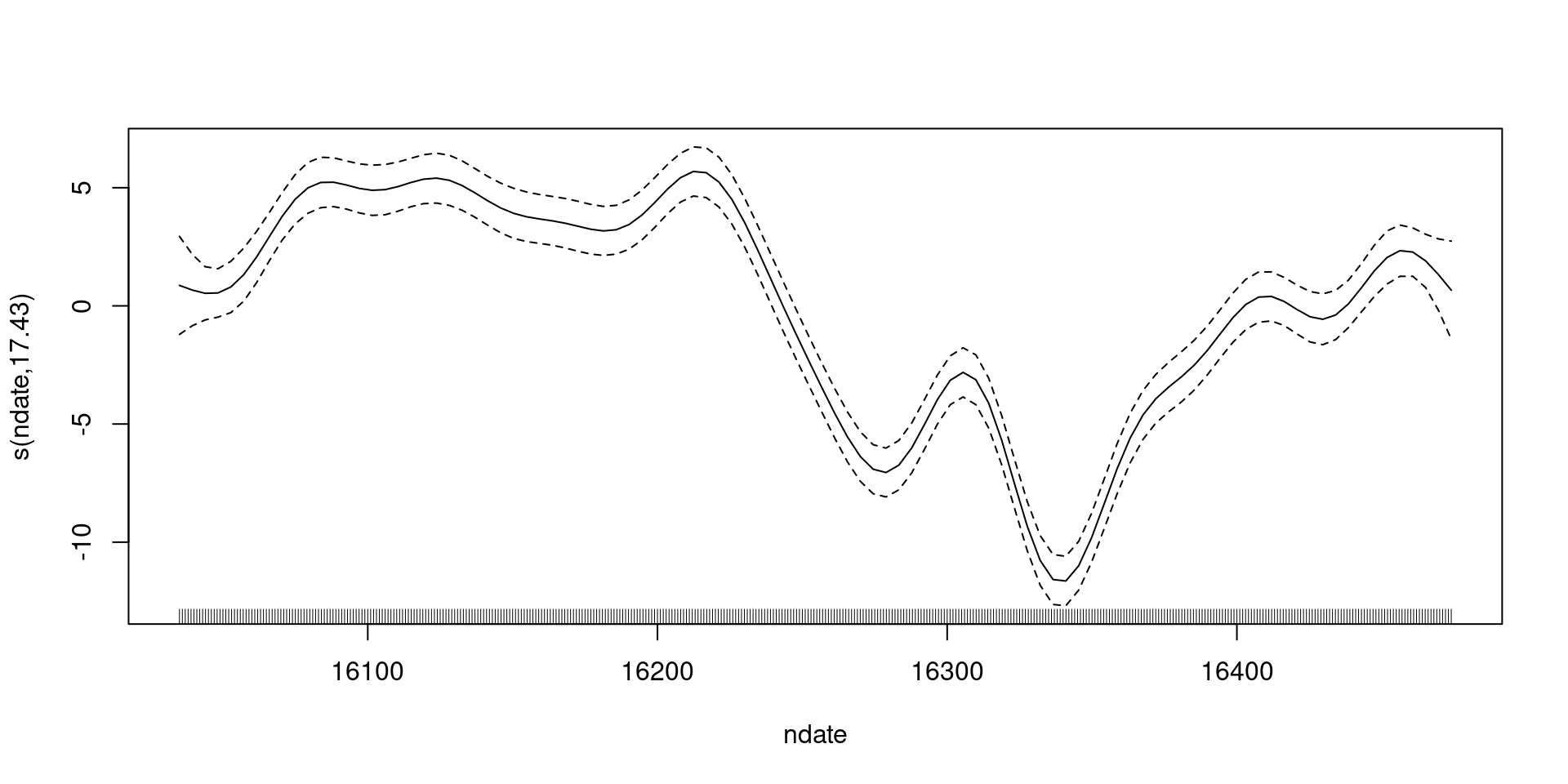
 18.6422253 -12.5062881

Wait, what are we seeing in that plot?

What do we have?

  • The black line: s(nday)
    • (what about \(\beta_0\)?)
  • Dashed line: s(nday) \(\pm 2\) standard errors
    • (how do we get to that?)
    • (what uncertainty is included?)

shifting to include the intercept

plot(b, shift=coef(b)[1])

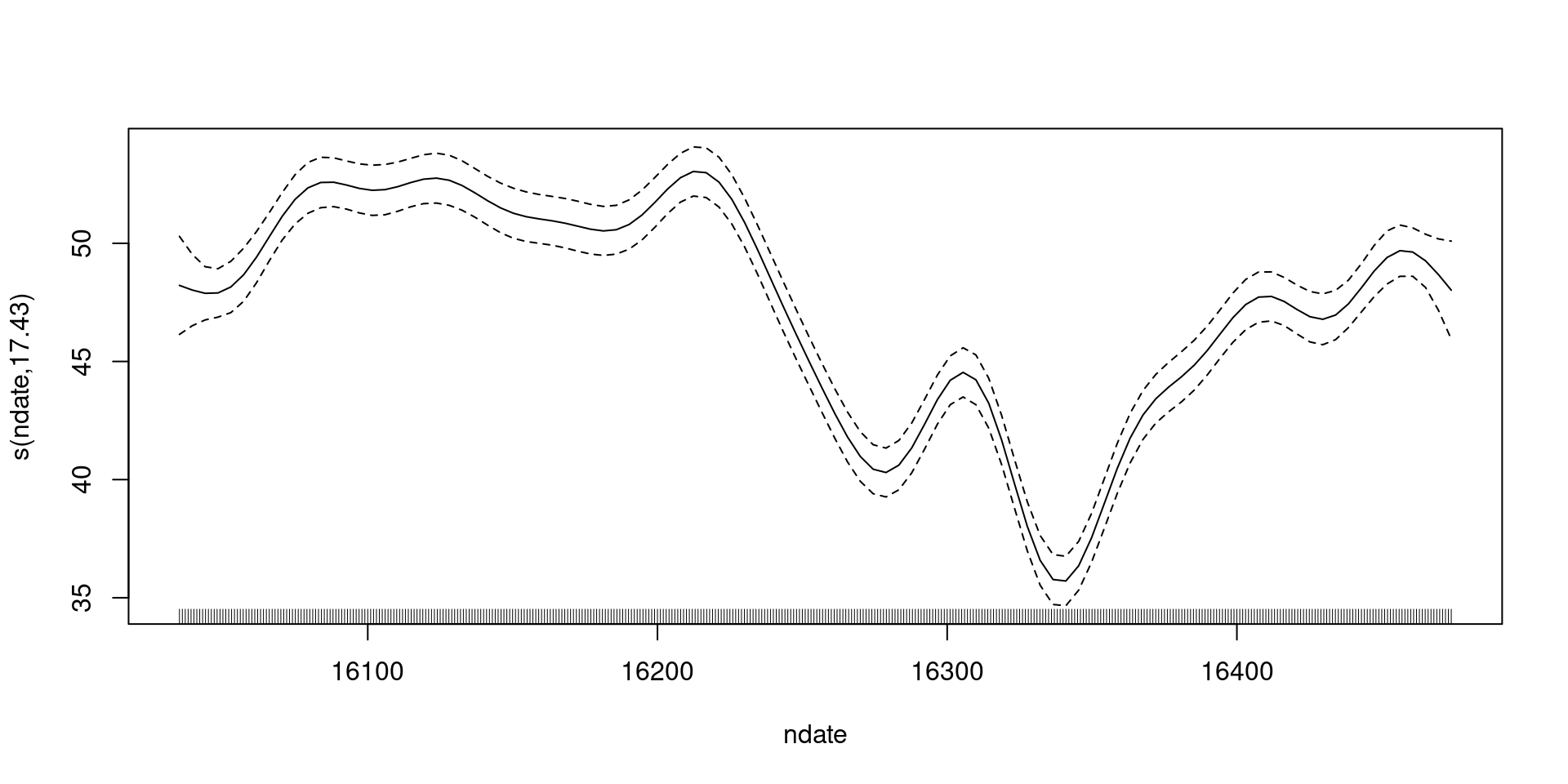
Including uncertainty in the intercept

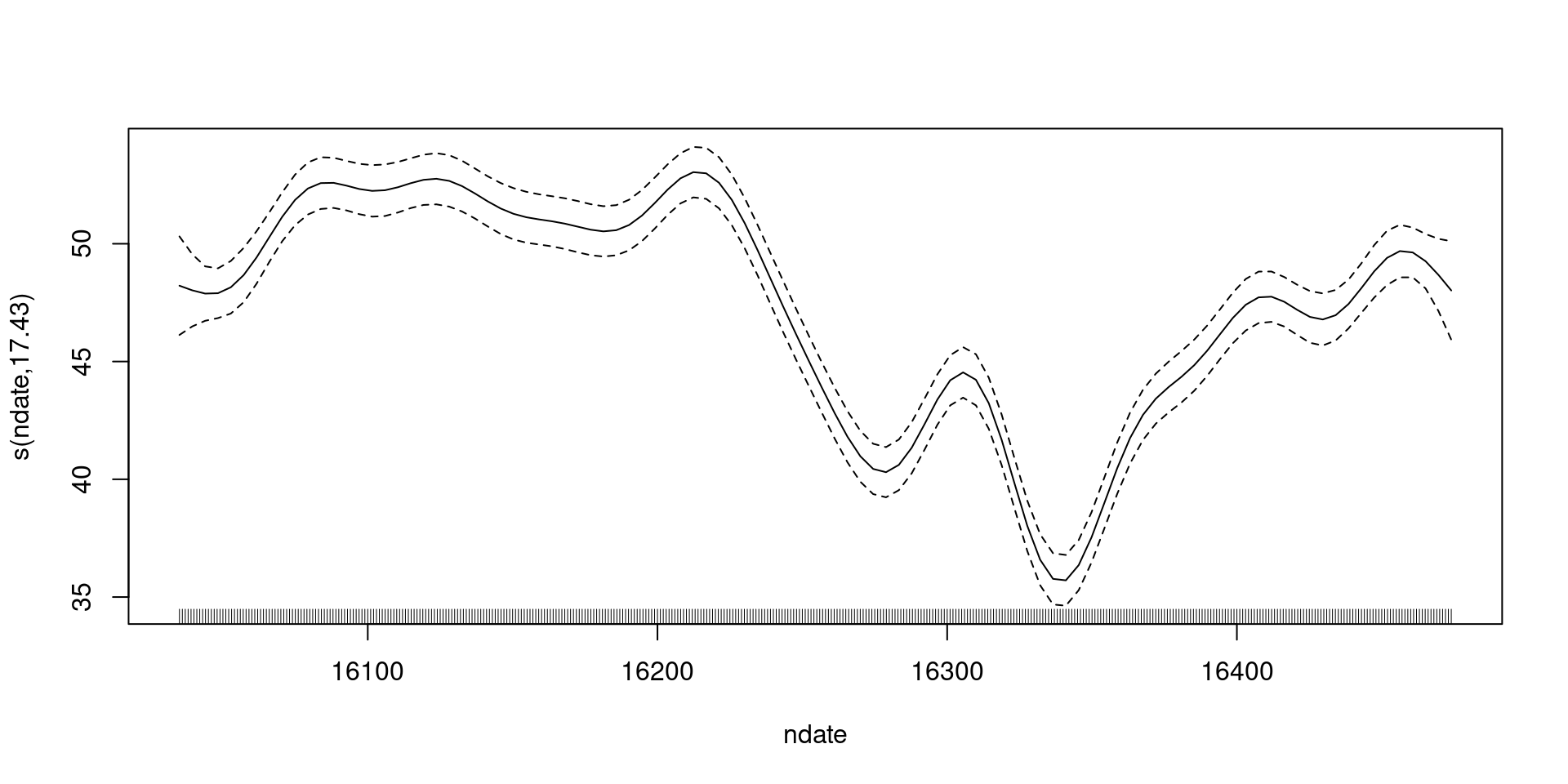
plot(b, shift=coef(b)[1], seWithMean=TRUE)

How do we make these plots?

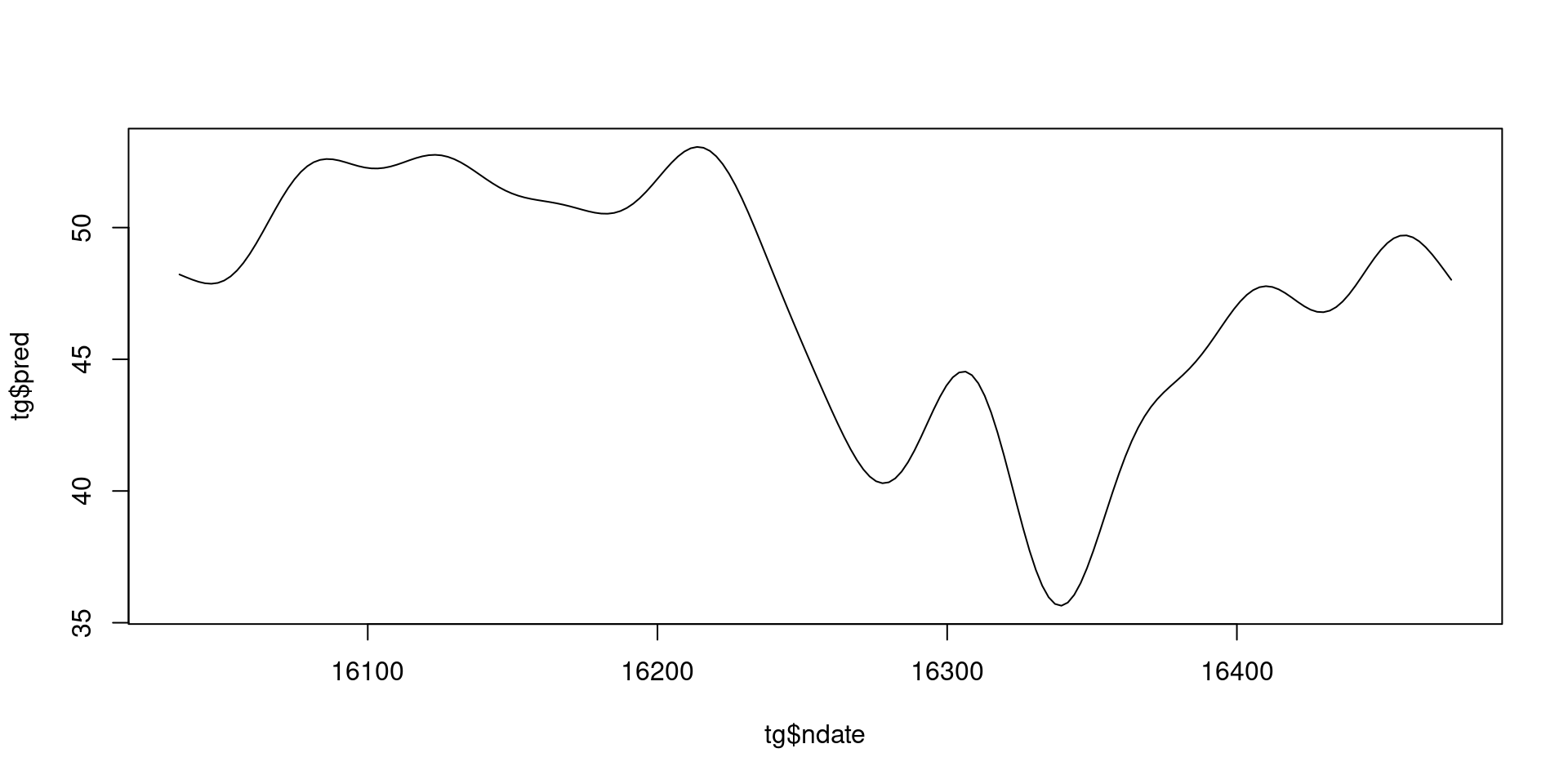
  • Black line is a prediction
  • \(\beta_0 + s(t)\) over values of \(t\)

How do we make these plots?

  • Black line is a prediction
  • \(\beta_0 + s(t)\) over values of \(t\)

Recipe:

  • Make a grid
  • Use predict() to make predictions over the grid

Doing that in R

tg <- data.frame(ndate=seq(min(wwoods$ndate),
                           max(wwoods$ndate),
                           length.out=200))

tg$pred <- predict(b, newdata=tg)

head(tg)
     ndate     pred
1 16035.00 48.21948
2 16037.21 48.11878
3 16039.41 48.02307
4 16041.62 47.94130
5 16043.82 47.88511
6 16046.03 47.86695

Doing that in R (extra bits)

  • Note that our newdata= needs to have all the covariates in it
  • Calling predict(b) just gives us fitted values

And we can plot that…

plot(tg$ndate, tg$pred, type="l")

What about uncertainty?

predict(..., se=TRUE) gives standard errors

tg_se <- predict(b, tg, se=TRUE)

str(tg_se)
List of 2
 $ fit   : num [1:200(1d)] 48.2 48.1 48 47.9 47.9 ...
  ..- attr(*, "dimnames")=List of 1
  .. ..$ : chr [1:200] "1" "2" "3" "4" ...
 $ se.fit: num [1:200(1d)] 1.046 0.899 0.767 0.657 0.579 ...
  ..- attr(*, "dimnames")=List of 1
  .. ..$ : chr [1:200] "1" "2" "3" "4" ...

Building that plot

plot(tg$ndate, tg$pred, type="l")
lines(tg$ndate, tg$pred + 2*tg_se$se.fit, lty=2)
lines(tg$ndate, tg$pred - 2*tg_se$se.fit, lty=2)

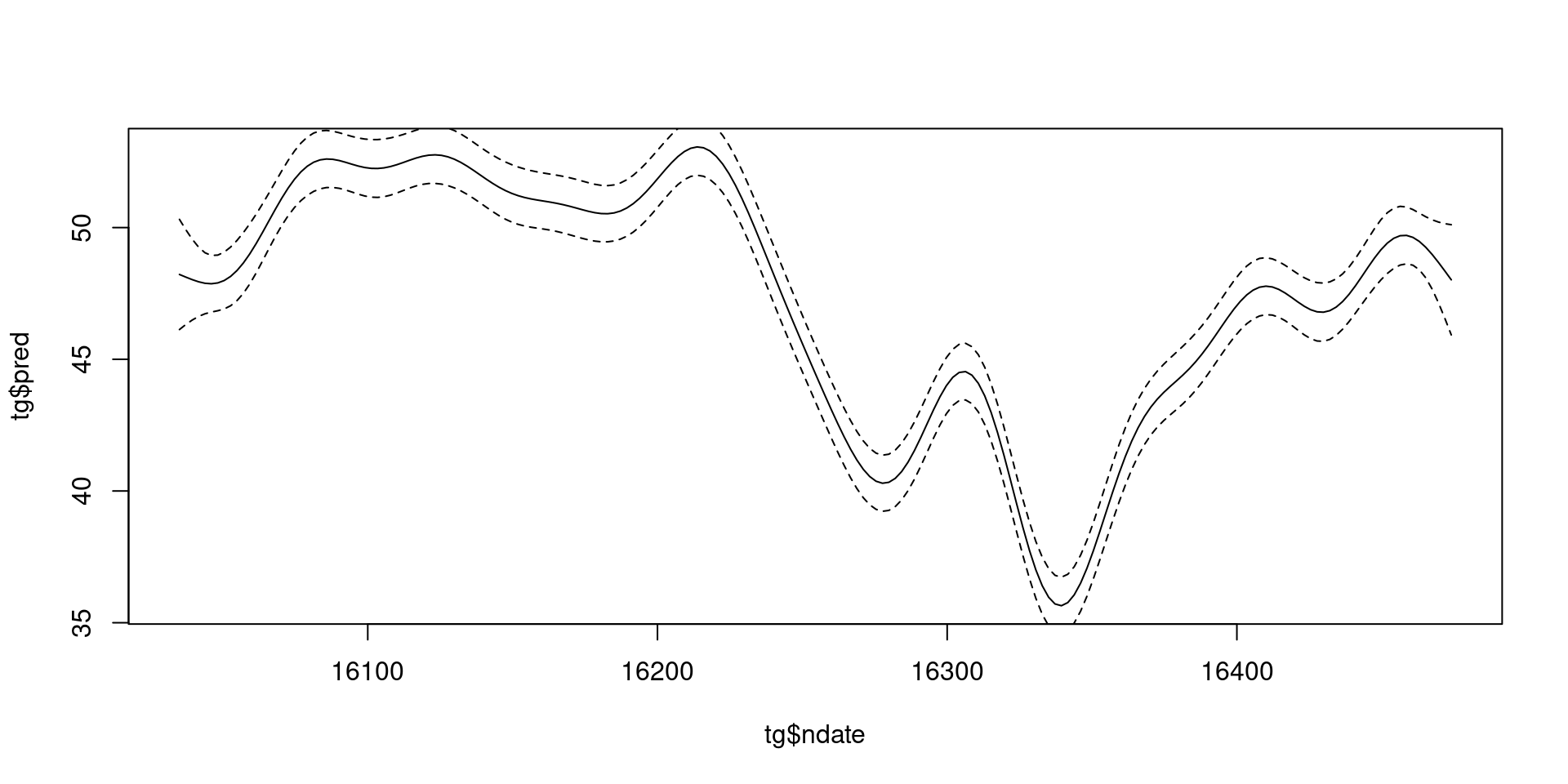
What do these intervals mean?

  • These are really credible intervals
    • … but they have good 🎲frequentist🎲 properties
    • (so we can call them confidence intervals)


  • What do they say?
    • they are “across-the-function” intervals
    • thinking about if \(s(x) = 0 \quad \forall x\)
      • (a bit more complicated becuase of centering)
    • see summary()

Thinking about intervals…

  • Why are they credible intervals?
  • Because we can think of the penalty as a prior
  • Then we have a posterior for our model
  • … and we can do 🔮posterior sampling🔮
    • (more on that in a minute)

Where did that uncertainty come from?

  • So far we’re only looking at uncertainty from \(\hat{\boldsymbol{\beta}}\)
  • What about smoothing paramter (\(\lambda\)) uncertainty?
    • We estimate a parameter, we need some uncertainty!
  • For predict() and plot() we can use unconditional=TRUE
    • (doesn’t make a difference for this data)

Posterior sampling

Posterior sampling background

  • From ⚡theory⚡ \(\boldsymbol{\beta} \sim \text{MVN}(\hat{\boldsymbol{\beta}}, \Sigma)\)

  • So, we can 🔮simulate🔮 from that distribution

  • Make lots of predictions

    • make a prediction matrix and multiply by the simulated parameters

  • This generalizes very well, so we can make predictions of more than just smooths

  • Miller et al (2022) and Miller (2021) have more details

More on predict()

  • We’ll use more features of predict() later
  • type= argument changes the type of prediction
    • By default on the link scale (fine here for normal)
    • "response" to put on the response scale
    • "iterms" to give per term predictions
    • "lpmatrix" for a prediction matrix
    • Don’t worry about this for now!

Recap

  • plot shows us basic plots
    • we can make them ourselves if we want!
  • Make predictions using predict()
    • Need to fiddle to make the data
  • Use se.fit=TRUE to get uncertainty
    • unconditional=TRUE give us smoothing parameter uncertainty
  • Uncertainty comes from smooth parameters and smoothing parameters
  • Intervals can be used to check if the smooth is zero