plot(b$y, fitted(b), asp=1)
abline(a=0, b=1, lwd=2, col="red")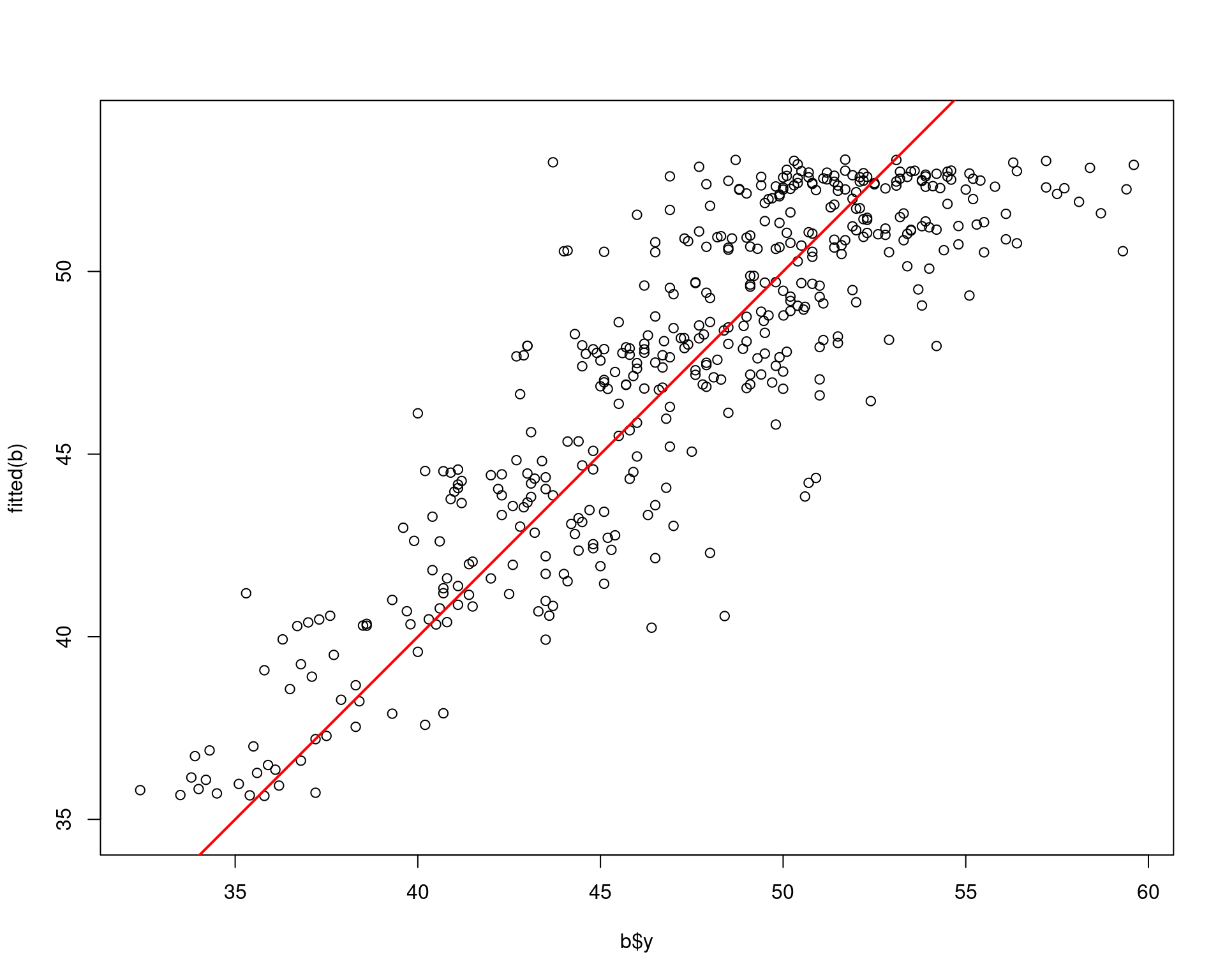
Biomathematics and Statistics Scotland
UK Centre for Ecology and Hydrology
blockCV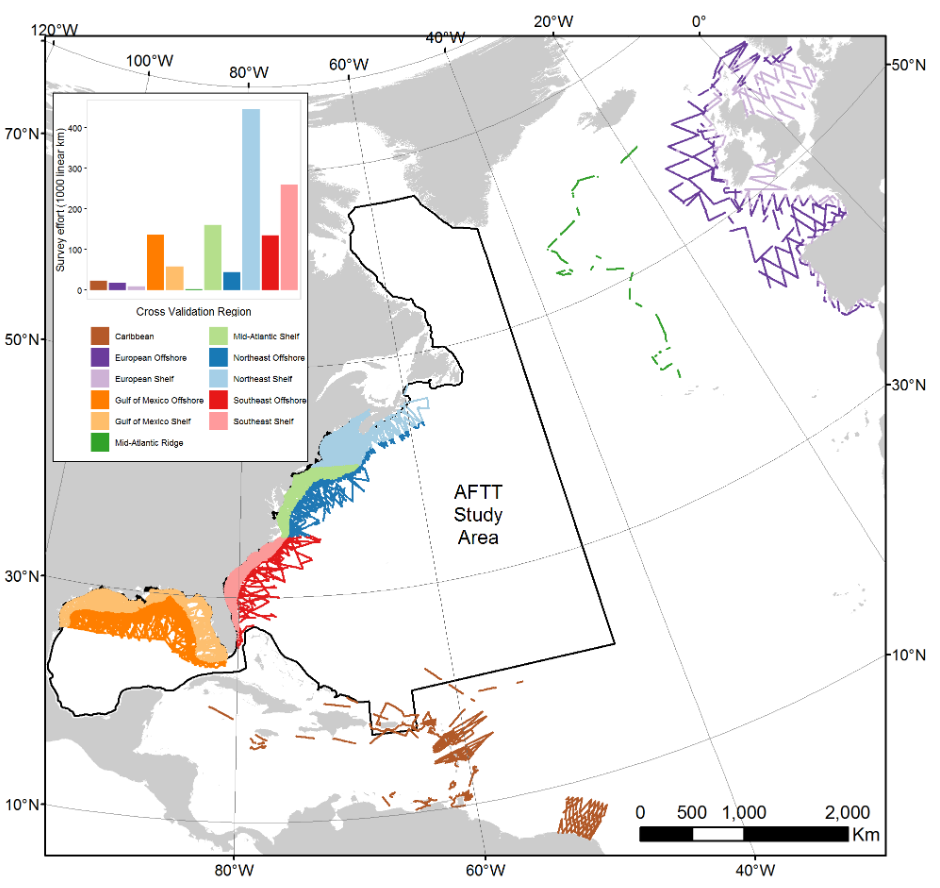
\[ \epsilon_i^D = \text{sign}(y_i - \mu_i)\sqrt{d_i} \]
where \(y_i\) is data, \(\mu_i\) is prediction and \(d_i\) is the deviance for observation \(i\)
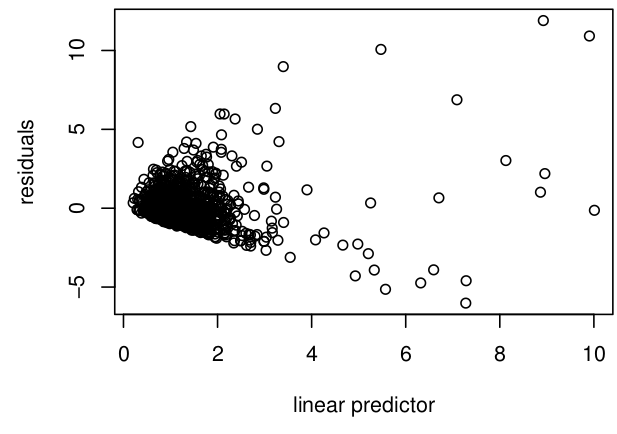
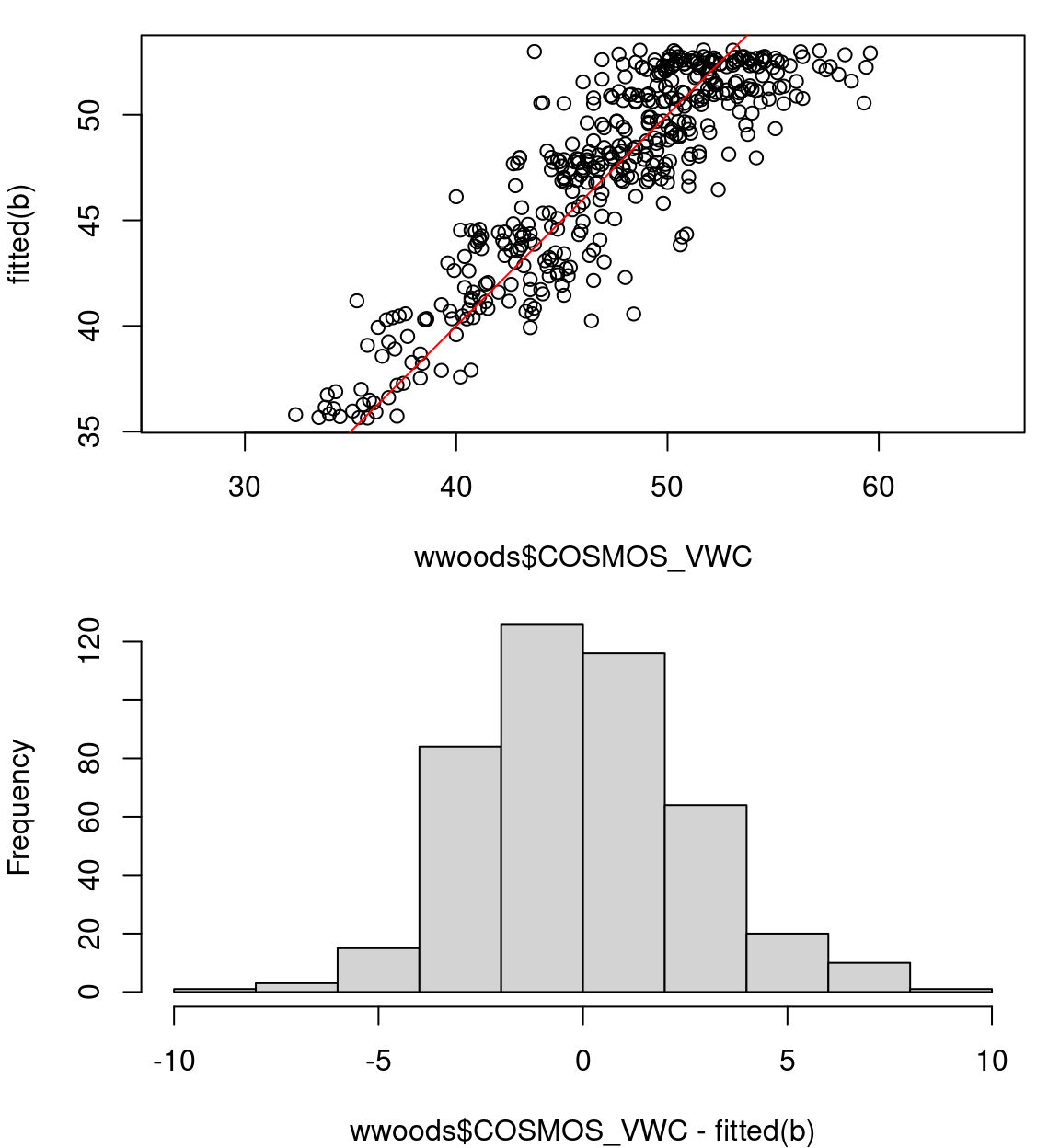
gam.check() 👌b0: COSMOS_VWC ~ s(ndate)b1: COSMOS_VWC ~ s(ndate) + s(SITE_ID, bs="re")AIC() in R: df AIC
b0 10.68555 122738.4
b1 15.89472 109391.2b1 is the better model!
Family: gaussian
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate) + s(SITE_ID, bs = "re") + s(ALTITUDE, k = 5) +
SOIL_TYPE
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40.991 4.860 8.435 <2e-16 ***
SOIL_TYPEOrganic soil 3.909 17.766 0.220 0.826
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(ndate) 8.841 8.992 165.575 <2e-16 ***
s(SITE_ID) 2.999 3.000 4753.831 <2e-16 ***
s(ALTITUDE) 1.000 1.000 0.174 0.676
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.579 Deviance explained = 57.9%
-REML = 54725 Scale est. = 49.913 n = 16208s(ALTITUDE) is not needed?\[ \lambda \int_\mathbb{R} \left( \frac{\partial^2 s(x)}{\partial x^2}\right)^2 \text{d}x\\ \]
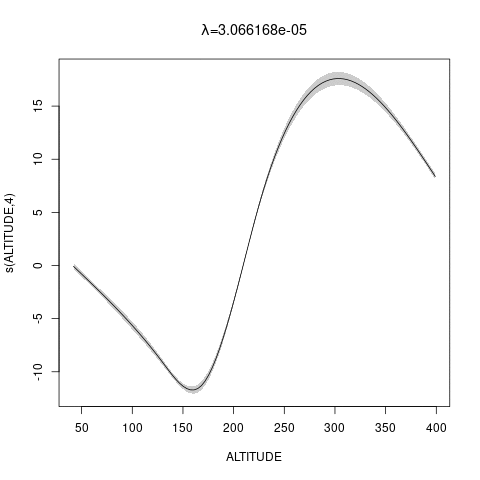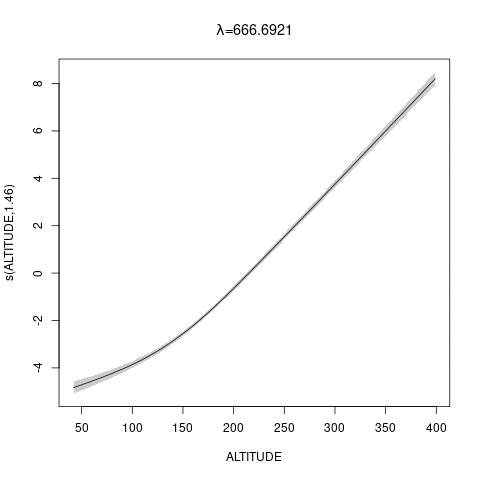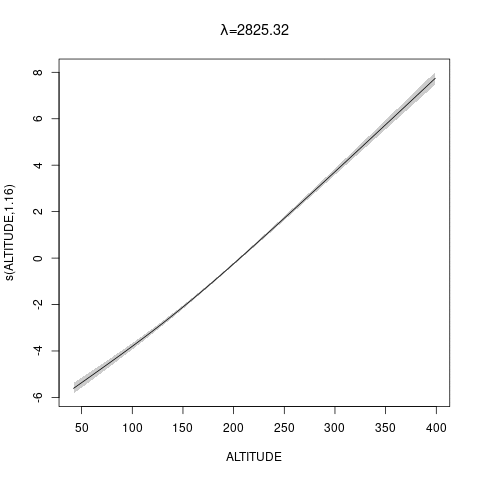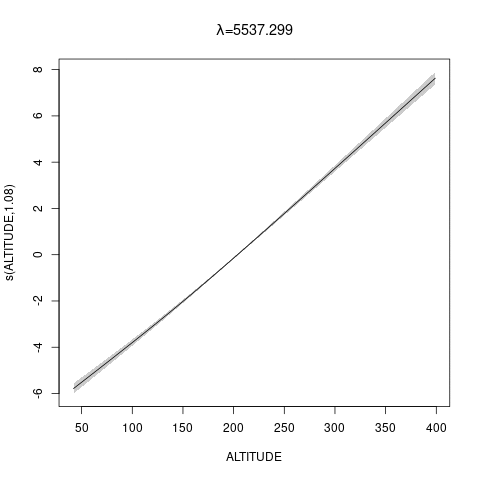
bs="ts" as we make \(\lambda\) bigger, then penalty works for nullspace terms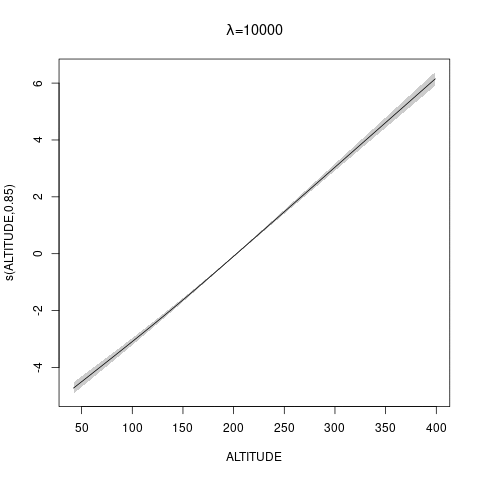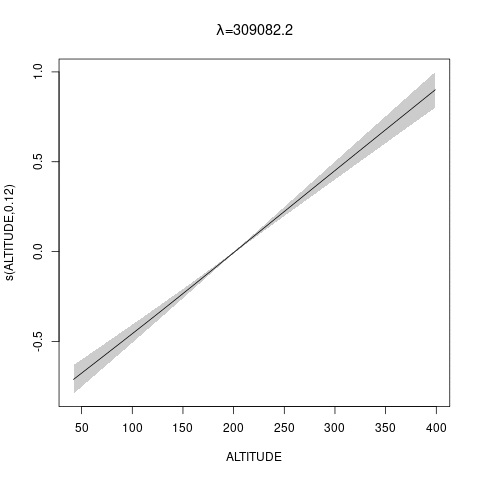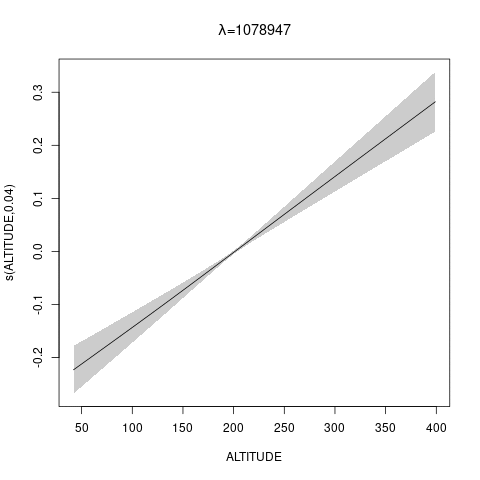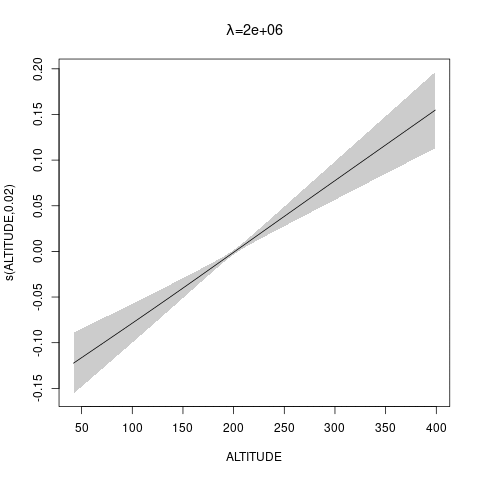
Family: gaussian
Link function: identity
Formula:
COSMOS_VWC ~ s(ndate) + s(SITE_ID, bs = "re") + s(ALTITUDE, k = 5,
bs = "ts") + SOIL_TYPE
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 39.821 3.550 11.216 <2e-16 ***
SOIL_TYPEOrganic soil 10.113 8.698 1.163 0.245
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(ndate) 8.8413793 8.992 165.574 <2e-16 ***
s(SITE_ID) 3.9983209 4.000 3777.345 <2e-16 ***
s(ALTITUDE) 0.0002275 4.000 0.008 0.637
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.579 Deviance explained = 57.9%
-REML = 54728 Scale est. = 49.913 n = 16208s(ALTITUDE) anyway
s(SITE_ID, bs="re") handles all the variationgam.check to see residual diagnosticsAIC() works like you expectbs="ts"